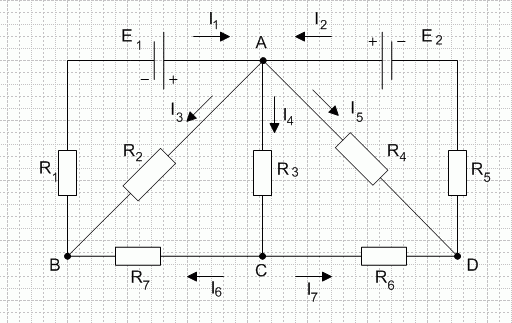
Кирхгофа 2 закон — это одно из основных правил электрической цепи, сформулированное немецким физиком Густавом Кирхгофом. Он утверждает, что сумма всех напряжений в замкнутом контуре равна нулю. То есть, если взять замкнутую электрическую цепь, то сумма разностей потенциалов на всех соединяющих ее элементах будет равна нулю.
Формула Кирхгофа 2 закона:
∑(V) = 0
Где ∑(V) — сумма всех напряжений в замкнутой электрической цепи.
Кирхгофа 2 закон находит свое применение в решении различных электрических цепей. Он позволяет находить неизвестные напряжения в замкнутом контуре, основываясь на известных значениях разностей потенциалов.
Давайте рассмотрим пример использования Кирхгофа 2 закона. Представим, что у нас есть электрическая цепь, состоящая из нескольких резисторов, батареи и проводников. Задача состоит в том, чтобы найти напряжение на определенном элементе цепи. Для этого мы можем применить Кирхгофа 2 закон, суммируя все напряжения в замкнутом контуре и приравнивая их к нулю. Зная значения всех остальных напряжений в цепи, мы сможем найти искомое напряжение.
Таким образом, Кирхгофа 2 закон является мощным инструментом для решения сложных задач в области электричества. Он позволяет анализировать электрические цепи и находить неизвестные величины с использованием простых математических операций.
Формула закона Кирхгофа 2
Математически формула закона Кирхгофа 2 записывается следующим образом:
∑Iвт = ∑Iвых
где:
∑Iвт — сумма втекающих электрических токов,
∑Iвых — сумма вытекающих электрических токов.
Таким образом, формула закона Кирхгофа 2 позволяет определить распределение тока в узлах электрической цепи. Она основана на том, что количество заряда, входящего в узел, должно быть равно количеству заряда, выходящего из узла.
Применение закона Кирхгофа 2 может быть полезно при решении сложных электрических цепей, где необходимо определить неизвестные токи или напряжения. Эта формула позволяет создавать системы уравнений, которые могут быть решены для определения неизвестных величин.
Определение и объяснение
Закон Кирхгофа 2 является доказательством закона сохранения заряда: он предполагает, что все заряды, поступающие в узел, должны быть равны зарядам, выходящим из узла. Другими словами, закон утверждает, что все токи, входящие или выходящие из узла, являются полным представлением всех входящих и исходящих зарядов.
Этот закон может быть представлен математической формулой, говорящей, что алгебраическая сумма потенциалов каждого элемента в цепи вдоль контура должна быть равна нулю:
Закон Кирхгофа 2 широко используется в различных областях, связанных с электричеством и электроникой. Он позволяет анализировать и решать сложные электрические цепи и определять величины токов и напряжений в различных элементах и узлах цепи. Закон Кирхгофа 2 также лежит в основе создания и проектирования электрических схем и устройств.
Математическая формулировка
Согласно формулировке закона, в любом замкнутом контуре электрической цепи (петле) сумма алгебраических значений напряжений, встречающихся на элементах цепи, равна нулю.
Можно представить это математически следующим образом:
ΣU = 0
где ΣU — сумма алгебраических значений напряжений в замкнутой петле.
Этот закон позволяет выполнять различные расчеты в электрических цепях, такие как нахождение неизвестных величин токов или напряжений, установление соотношений между элементами цепи и т.д.
Примечание: Для правильного применения закона Кирхгофа 2 важно учитывать знаки напряжений, выделять направление положительного тока и правильно обозначать напряжения на элементах цепи.
Примеры использования закона Кирхгофа 2
Пример 1:
| Цепь | Значение сопротивления (Ом) | Ток (А) |
| 1 | 10 | 2 |
| 2 | 20 | ? |
| 3 | 30 | 5 |
В данном примере известны значения сопротивлений цепей 1 и 3, а также значение тока в цепи 1. С помощью закона Кирхгофа 2 можно определить значение тока в цепи 2. Сумма алгебраических значений токов, входящих и выходящих из узла, равна нулю. Таким образом, ток в цепи 2 можно вычислить, зная ток в цепи 1 и 3.
Пример 2:
| Цепь | Значение сопротивления (Ом) | Ток (А) |
| 1 | 5 | ? |
| 2 | 10 | 3 |
| 3 | 15 | 2 |
В этом примере известны значения сопротивлений цепей 2 и 3, а также значения токов в этих цепях. С помощью закона Кирхгофа 2 можно определить значение тока в цепи 1. Сумма алгебраических значений токов, входящих и выходящих из узла, равна нулю. Таким образом, ток в цепи 1 можно вычислить, зная токи в цепях 2 и 3.
Примеры использования закона Кирхгофа 2 помогают решать сложные задачи, связанные с определением значений токов в разветвленных цепях.
Пример схемы электрической цепи
Для наглядного представления работы закона Кирхгофа 2, рассмотрим следующую схему электрической цепи:
В данной схеме имеется два источника тока, обозначенных И1 и И2, соответственно. Также в цепи присутствуют три сопротивления, обозначенные Р1, Р2 и Р3, и два соединителя, обозначенные А и В.
Согласно закону Кирхгофа 2, сумма алгебраических значений электрических сил, действующих в узле цепи, равна нулю. Из этого следует, что сумма падений напряжения на всех резисторах в цепи равна сумме электрических сил.
Допустим, что источник тока И1 имеет электрическую силу E1, а источник тока И2 имеет электрическую силу E2. При наличии сопротивлений, на каждом из них будет присутствовать падение напряжения, обозначенное U1, U2 и U3.
В соответствии с законом Кирхгофа 2, уравнение для данной схемы будет выглядеть следующим образом:
E1 + E2 = U1 + U2 + U3
Таким образом, можно использовать закон Кирхгофа 2 для решения данного уравнения и определения значений напряжения на каждом из сопротивлений в электрической цепи.
Пример расчета с использованием формулы
Давайте рассмотрим пример расчета с использованием формулы, основываясь на Кирхгофовом законе 2.
Предположим, у нас есть электрическая цепь, состоящая из одного источника постоянного тока (ЭДС E) и двух резисторов (R1 и R2), подключенных последовательно.
По Кирхгофову закону 2 сумма падений напряжения на каждом резисторе равна напряжению источника:
V = V1 + V2
где V — напряжение источника, V1 — напряжение на первом резисторе, V2 — напряжение на втором резисторе.
Напряжение на резисторе можно рассчитать с помощью формулы:
V = I * R
где I — сила тока, проходящего через резистор, R — сопротивление резистора.
Предположим, что сила тока, проходящего через цепь, составляет 1 Ампер, а значение сопротивления первого резистора равно 3 Ома, а второго — 5 Ом.
Рассчитаем напряжение на каждом резисторе:
| Резистор | Сопротивление (Ом) | Напряжение (Вольт) |
|---|---|---|
| R1 | 3 | 3 |
| R2 | 5 | 5 |
Сумма напряжений на обоих резисторах равна напряжению источника:
3 + 5 = 8 Вольт
Таким образом, с использованием формул Кирхгофа 2 закона мы смогли рассчитать напряжение на каждом резисторе и убедиться в справедливости закона.
Пример практического применения
Уравнение Кирхгофа 2 закона широко используется в электрических цепях для анализа тока и напряжения. Например, пусть у нас есть электрическая цепь, состоящая из двух резисторов и батареи. Нам нужно найти значение тока, протекающего через резисторы.
Используя закон Ома, мы можем выразить значения напряжения на каждом резисторе в зависимости от тока и сопротивления. Затем, применяя закон Кирхгофа 2, мы можем составить уравнение:
U1 — I*R1 — I*R2 = 0
Где U1 — напряжение на батарее, I — значение тока, протекающего через резисторы, R1 и R2 — значения сопротивления резисторов.
Решая это уравнение, мы можем найти значение тока I. Таким образом, мы можем определить, какое количество тока будет протекать через каждый из резисторов.
Практическое применение закона Кирхгофа 2 включает в себя расчеты в электрических схемах, проектирование электрических цепей и определение показателей электрической безопасности. Применение этого закона позволяет инженерам и электрикам более эффективно планировать и контролировать электрические системы.
Применение закона Кирхгофа 2 в различных областях
В области электротехники закон Кирхгофа 2 применяется при расчете сложных электрических цепей, состоящих из нескольких параллельно соединенных элементов, таких как резисторы, конденсаторы и индуктивности. Этот закон позволяет определить значения токов в различных участках цепи, а также рассчитать электрические параметры цепей, такие как общее сопротивление или емкость.
Закон Кирхгофа 2 также находит применение в оптике. В оптических системах, таких как линзы, зеркала и оптические приборы, этот закон используется для определения распределения интенсивности света в различных точках системы. Он позволяет рассчитать путь световых лучей, проходящих через оптические элементы, а также вычислить фокусные расстояния или геометрические параметры системы.
Другой областью, где применяется закон Кирхгофа 2, является акустика. Этот закон позволяет анализировать распространение звуковых волн в замкнутых пространствах, таких как помещения или звуковые системы. Он помогает определить амплитуды и фазы звуковых волн, а также рассчитать их распространение и отражение от поверхностей.
Также закон Кирхгофа 2 находит применение в теплотехнике. В системах тепло- и массообмена, таких как теплообменники и парогенераторы, этот закон используется для определения распределения тепла и массы в системе. Он позволяет рассчитать температурные и концентрационные профили, а также определить эффективность теплообмена.
Таким образом, закон Кирхгофа 2 является универсальным инструментом анализа и расчета в различных областях науки и техники, где требуется определение распределения физических величин в сложных системах. Его применение позволяет получить точные и надежные результаты и играет важную роль в развитии современной технологии.
Вопрос-ответ:
Как формулируется второй закон Кирхгофа?
Второй закон Кирхгофа утверждает, что в любой замкнутой электрической цепи алгебраическая сумма падений напряжения на всех элементах цепи равна алгебраической сумме электродвижущих сил.
Какова формула второго закона Кирхгофа?
Формула второго закона Кирхгофа выглядит так: Σ(Emf) = Σ(IR), где Σ(Emf) — алгебраическая сумма электродвижущих сил, Σ(IR) — алгебраическая сумма падений напряжения.
Как применяется второй закон Кирхгофа в практике?
Второй закон Кирхгофа применяется в практике для анализа сложных электрических цепей. С его помощью можно рассчитать падения напряжения на различных элементах цепи и определить токи, проходящие через каждый из них.
Можете привести пример применения второго закона Кирхгофа?
Допустим, у нас есть электрическая цепь, состоящая из нескольких резисторов, источника электродвижущей силы и ключа. По второму закону Кирхгофа можно рассчитать ток, проходящий через каждый резистор, зная значения сопротивлений и электродвижущей силы источника.
Какой принцип лежит в основе второго закона Кирхгофа?
Принцип сохранения энергии лежит в основе второго закона Кирхгофа. Согласно этому принципу, электродвижущая сила, создаваемая источником энергии, компенсируется падением напряжения на резисторах в цепи.
Что такое Кирхгофа 2 закон?
Кирхгофа 2 закон — это физический закон из области электротехники, утверждающий, что алгебраическая сумма токов в узле электрической цепи равна нулю.