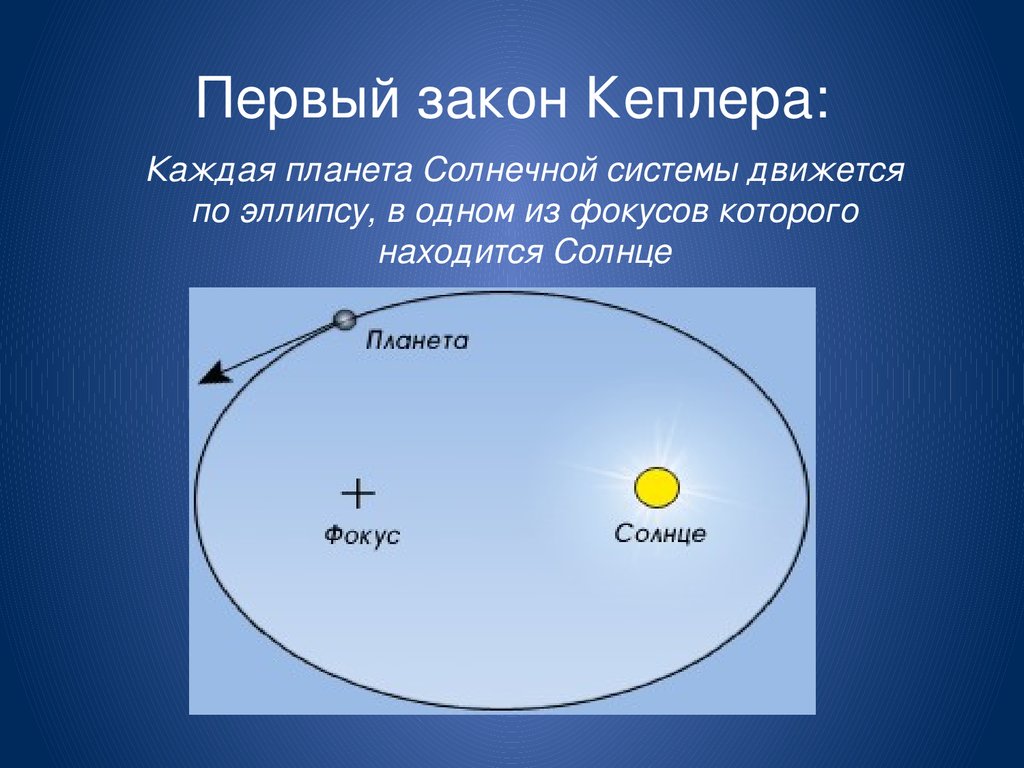
Третий закон Кеплера – одно из фундаментальных открытий в астрономии, сделанное немецким астрономом и математиком Иоганном Кеплером в начале семнадцатого века. Этот закон относится к описанию движения планет вокруг Солнца и определяет зависимость между периодом обращения планеты вокруг Солнца и её средним расстоянием от Солнца.
Основой третьего закона Кеплера является давно установленный закон всемирного тяготения, открытый Исааком Ньютоном. Закон всемирного тяготения утверждает, что массы двух тел прямо пропорциональны, а силы, действующие между этими телами, обратно пропорциональны квадрату расстояния между ними. Исходя из этого закона, Кеплер смог установить, что средние расстояния планет от Солнца связаны с их периодами обращения вокруг Солнца простой математической зависимостью.
Запишем третий закон Кеплера математически. Пусть Т — период обращения одной планеты вокруг Солнца, а R — среднее расстояние этой планеты от Солнца. Тогда, согласно третьему закону Кеплера, квадрат периода обращения Т в секундах равен кубу среднего расстояния R в астрономических единицах.
Третий закон Кеплера в астрономии
Согласно третьему закону Кеплера, квадрат периода обращения планеты вокруг Солнца пропорционален кубу среднего расстояния между ними. Другими словами, время, которое занимает планете для завершения одного обращения вокруг Солнца (период), связано с ее средним расстоянием от Солнца (большой полуосью орбиты).
Значение третьего закона Кеплера заключается в том, что он позволяет астрономам определять характеристики планет и других небесных объектов, основываясь только на наблюдаемых данных. С его помощью можно вычислить орбитальные периоды и расстояния от Солнца к планетам, что позволяет более точно описывать и предсказывать их движение и положение. Третий закон Кеплера также является основой для формулирования законов гравитации Ньютона и важным элементом в нашем понимании общей структуры и развития Вселенной.
История открытия
Кеплеру удалось сформулировать этот закон после многолетнего анализа наблюдений и данных, собранных его предшественниками астрономами. В течение многих лет Кеплер систематически изучал движение планет, записывая огромное количество данных и анализируя их. За годы своей работы он обнаружил определенные закономерности и установил, что существует связь между периодом обращения планеты вокруг Солнца, длиной большой полуоси ее орбиты и массой Солнца.
Открытие третьего закона Кеплера имело огромное значение в астрономии. Оно позволило более точно определить орбиты планет и установить закономерности в их движении. Также этот закон послужил фундаментом для дальнейших исследований и разработок в области космической астрономии и навигации. Сам Кеплер считал свое открытие одним из самых важных моментов в истории науки.
Открытие закона
Третий закон Кеплера, также известный как закон гармонии, был открыт немецким астрономом Иоганном Кеплером в начале 17 века. Он был последним из трех законов Кеплера, которые описывают движение планет вокруг Солнца.
Открытие третьего закона Кеплера стало значимым шагом вперед в астрономии и помогло лучше понять законы движения планет.
Иоганн Кеплер проводил многочисленные наблюдения и анализировал данные, собранные телескопами его времени. Он заметил, что есть пропорциональная зависимость между периодом обращения планеты вокруг Солнца и ее средним расстоянием до Солнца. Это значит, что чем больше расстояние до Солнца, тем больше времени понадобится планете для обращения вокруг него.
Используя свои наблюдения и математические расчеты, Кеплер вывел уравнение, которое объясняет эту зависимость и описывает закон гармонии.
Открытие закона Кеплера помогло установить основы для дальнейших исследований в астрономии и облегчило понимание механизмов движения планет. Сегодня этот закон является важной составляющей небесной механики и используется для расчетов и прогнозирования перемещения планет и других небесных тел.
Работа Иоганна Кеплера
Кеплер занимался исследованием движения планет, сформулировав три закона, которые получили его имя. Он отверг полностью геоцентрическую систему, предложившую геллиоцентрическую систему — что Солнце находится в центре Солнечной системы, а планеты вращаются вокруг него по эллиптическим орбитам.
Кеплер провел множество наблюдений, включая изучение Марса и Венеры. Он сделал ряд открытий, вносящих существенный вклад в развитие астрономии. Например, он установил, что планеты движутся быстрее в ближайшей точке к Солнцу (перигелии) и медленнее в дальнейшей точке (афелии).
Кеплер также создал первые точные таблицы планетарных движений и разработал математический метод, позволяющий с высокой точностью предсказывать положение планет на определенный момент времени.
Его работы стали основополагающими для дальнейшего развития астрономии и обусловили ряд открытий исследователей, таких как Ньютон. Он сумел соединить наблюдение с математикой и физикой, создав научную основу для понимания законов природы.
Иоганн Кеплер внес огромный вклад в развитие астрономии и наук в целом своими открытиями и работой над законами движения планет. Его научные исследования и теории оказали существенное влияние на наши знания о Вселенной и стали отправной точкой для дальнейших открытий.
Особенности
Третий закон Кеплера, также известный как закон периодов, имеет несколько особенностей и интересных свойств:
| Соотношение периодов | В соответствии с третьим законом Кеплера, отношение квадрата периода обращения двух планет к кубу их средних расстояний равно постоянной величине. Это означает, что период обращения планеты пропорционален третьему корню от среднего расстояния от Солнца. Такое соотношение позволяет установить закономерности и регулярности в движении небесных тел и прогнозировать их положение в будущем. |
| Универсальность | Третий закон Кеплера справедлив не только для планет Солнечной системы, но и для других небесных тел, таких как спутники, астероиды, кометы и даже галактики. Это обнаружение позволяет астрономам использовать третий закон Кеплера для изучения и анализа движения различных космических объектов, не только в нашей Солнечной системе, но и во всей Вселенной. |
| Подтверждение теории гравитации | Третий закон Кеплера был открыт задолго до того, как была сформулирована теория гравитации Исааком Ньютоном. Однако он оказался совместимым с этой теорией и даже подтвердил ее. Третий закон Кеплера дает количественную формулировку связи между силой гравитации, массой небесного тела и его орбитой. Поэтому он стал одной из основных поддержек теории гравитации Исаака Ньютона. |
Математическая формула
Математическая формула, описывающая третий закон Кеплера, выглядит следующим образом:
- При движении планеты вокруг Солнца, квадрат периода обращения планеты прямо пропорционален кубу большой полуоси ее орбиты.
- Математически это можно записать как T2 = k * a3, где T — период обращения планеты вокруг Солнца, a — большая полуось орбиты планеты, k — постоянная пропорциональности.
Такая формула позволяет связать два основных параметра орбиты планеты и определить их взаимосвязь. Третий закон Кеплера является важным эмпирическим законом, который позволил описать движение планет в Солнечной системе и открыть новые закономерности в астрономии.
Зависимость от массы
Третий закон Кеплера описывает зависимость периода обращения планеты вокруг Солнца от ее массы. Согласно закону, период обращения планеты возрастает с увеличением ее массы. Это означает, что планеты с большей массой имеют более длительный период обращения вокруг Солнца.
Эта зависимость объясняется гравитационными силами, действующими между планетой и Солнцем. Чем больше масса планеты, тем сильнее ее притяжение на Солнце, что влияет на ее скорость движения вокруг него. Следовательно, планеты с большей массой движутся медленнее и имеют более длительный период обращения.
Зависимость от массы также влияет на форму орбиты планеты. Планеты с большей массой имеют менее эксцентричные орбиты, более близкие к круговым, в отличие от планет с меньшей массой, у которых орбиты могут быть более вытянутыми и эксцентричными. Это связано с тем, что большая масса планеты создает более сильное гравитационное притяжение, которое уравновешивается центробежной силой и обеспечивает более стабильную и круговую орбиту.
Соотношение между периодом обращения и расстоянием
Третий закон Кеплера гласит, что квадрат периода обращения планеты вокруг Солнца пропорционален кубу её среднего расстояния до Солнца. Это соотношение можно выразить следующей формулой:
T^2 = k * r^3
Где T — период обращения планеты, r — среднее расстояние до Солнца, а k — постоянная пропорциональности. Постоянная k зависит от системы единиц измерения, которую мы используем.
Закон Кеплера позволяет определить период обращения планеты, если известно её расстояние до Солнца, или наоборот, определить расстояние до Солнца, если известен период обращения. Этот закон играл важную роль в развитии астрономии, позволившей более точно определить параметры планетарных систем и движение планет.
Соотношение между периодом обращения и расстоянием также позволяет установить сравнительную длительность годов на разных планетах. Например, известно, что период обращения Земли составляет около 365 дней, а среднее расстояние от Земли до Солнца составляет примерно 1 астрономическую единицу (А.Е.). С использованием закона Кеплера можно рассчитать период обращения других планет и сравнить его с нашим годом.
Соотношение между периодом обращения и расстоянием является одним из ключевых открытий Кеплера и играет важную роль в современной астрономии. Оно помогает нам лучше понять движение планет и определить параметры планетарных систем, давая нам возможность изучать и понимать устройство вселенной.
Вопрос-ответ:
Какие открытия сделаны при исследовании третьего закона Кеплера?
В ходе исследования третьего закона Кеплера были сделаны следующие открытия: закон Гарио, который связывает период обращения планеты вокруг Солнца с её средним расстоянием от Солнца, а также закон Титиусла, который утверждает, что расстояния планет от Солнца пропорциональны их периодам обращения.
Какие особенности третьего закона Кеплера в астрономии?
Особенности третьего закона Кеплера в астрономии заключаются в том, что он описывает математическую зависимость между периодом обращения планеты вокруг Солнца и её средним расстоянием от Солнца. Также он позволяет определить соотношение периодов обращения различных планет вокруг Солнца.
Какое значение имеет третий закон Кеплера в астрономии?
Третий закон Кеплера имеет большое значение в астрономии, так как он позволяет определить период обращения планеты вокруг Солнца и её среднее расстояние от Солнца на основе эмпирических данных. Это позволяет установить закономерности в движении планет и улучшить наши знания об устройстве Солнечной системы.
Как называется закон Кеплера, который связывает период обращения планеты вокруг Солнца и её среднее расстояние от Солнца?
Закон Кеплера, который связывает период обращения планеты вокруг Солнца и её среднее расстояние от Солнца, называется законом Гарио. Он был сформулирован немецким астрономом Яном Гарио в 1619 году и является одним из трех законов Кеплера, описывающих движение планет вокруг Солнца.
Какие законы Кеплера определяют зависимость периода обращения планеты от её расстояния от Солнца?
Законы Кеплера, определяющие зависимость периода обращения планеты от её расстояния от Солнца, это закон Титиусла и закон Гарио. Закон Титиусла утверждает, что расстояния планет от Солнца пропорциональны их периодам обращения, а закон Гарио устанавливает математическую связь между периодом обращения планеты и её средним расстоянием от Солнца.